Principles of LLM Reliability

Understanding LLM Reliability

Large Language Models (LLMs) are enormously impressive and fundamentally flawed. Despite being very useful they unpredictably emit incorrect, incomplete, and capricious outputs. Achieving reliable performance objectives using LLMs requires harnessing their functionality within a carefully engineered system that mitigates the challenges.

Designing reliable systems from unreliable components is the quintessential engineering task, but it depends on understanding why the components are unreliable. Some of the most familiar flaws in LLMs are hallucinations, volatility, and instability. Hallucinations are outputs that seem to be factual but are actually synthetic. Volatility arises when a given input to an LLM gives different results on successive execution. Instability refers to behavior where small changes in the input cause much larger changes in the output.

This post explains why these flaws are inherent in current LLM architecture and derives a list of essential principles for using LLMs as a component in an engineered system.

LLMs as a Black Box

An LLM is a model of training data that can be used to generate statistically likely text outputs from arbitrary text inputs. The training data starts with a data corpus, which is a vast array of source material. This is processed by formatting, annotation, labeling, and other techniques to form the body of training data, which is used to train the model.

The actual training process is quite complex with pre-training, fine-tuning, etc. For this black box analysis we are concerned with the resulting model and the generation process, where we provide a text prompt and receive a text result. Here the training data represents the set of all information that has been made available to the model, both before and during the training process.

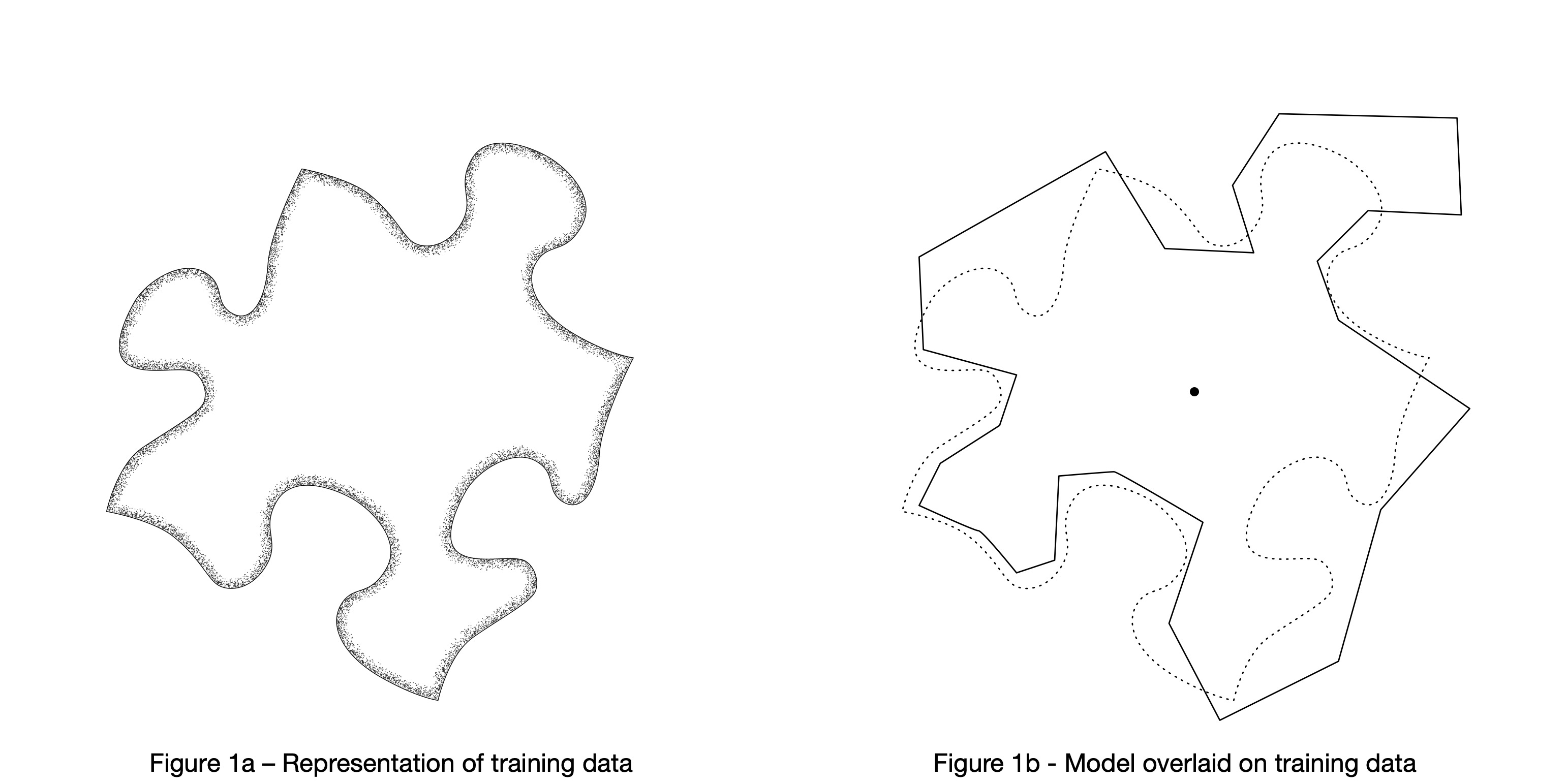
Figure 1a is a conceptual representation of a body of training data where the uneven boundaries represent the bounds of a vast amount of data. Everything the model can generate is based on something within the training data.

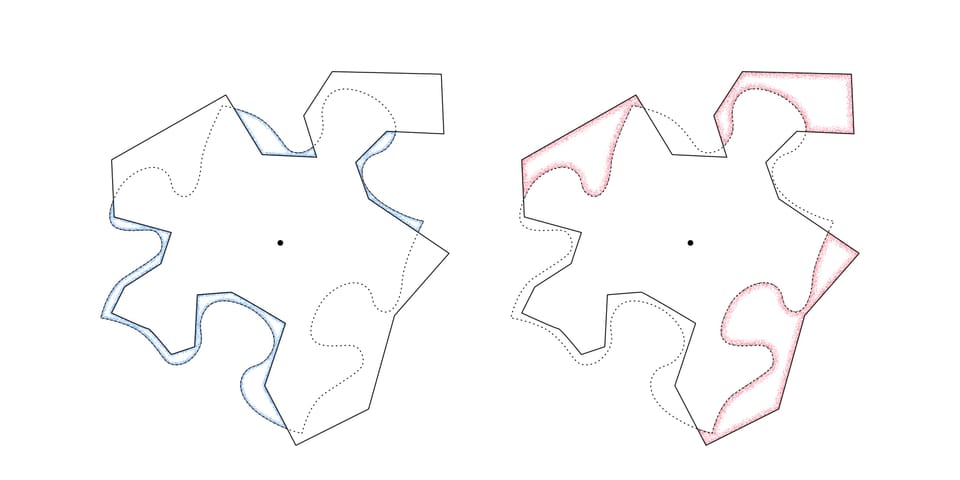
Figure 1b shows an LLM overlaid on the training data. The solid outline of the model contains the relationships among “tokens” that roughly corresponding to words. Every possible relationship among words or sequences of words has a statistical likelihood within the model. An important concept is that the model only “knows” its own information, as bounded by the solid line. It cannot determine if a given datum is within the bounds of the training data. The dotted line is just for illustration.

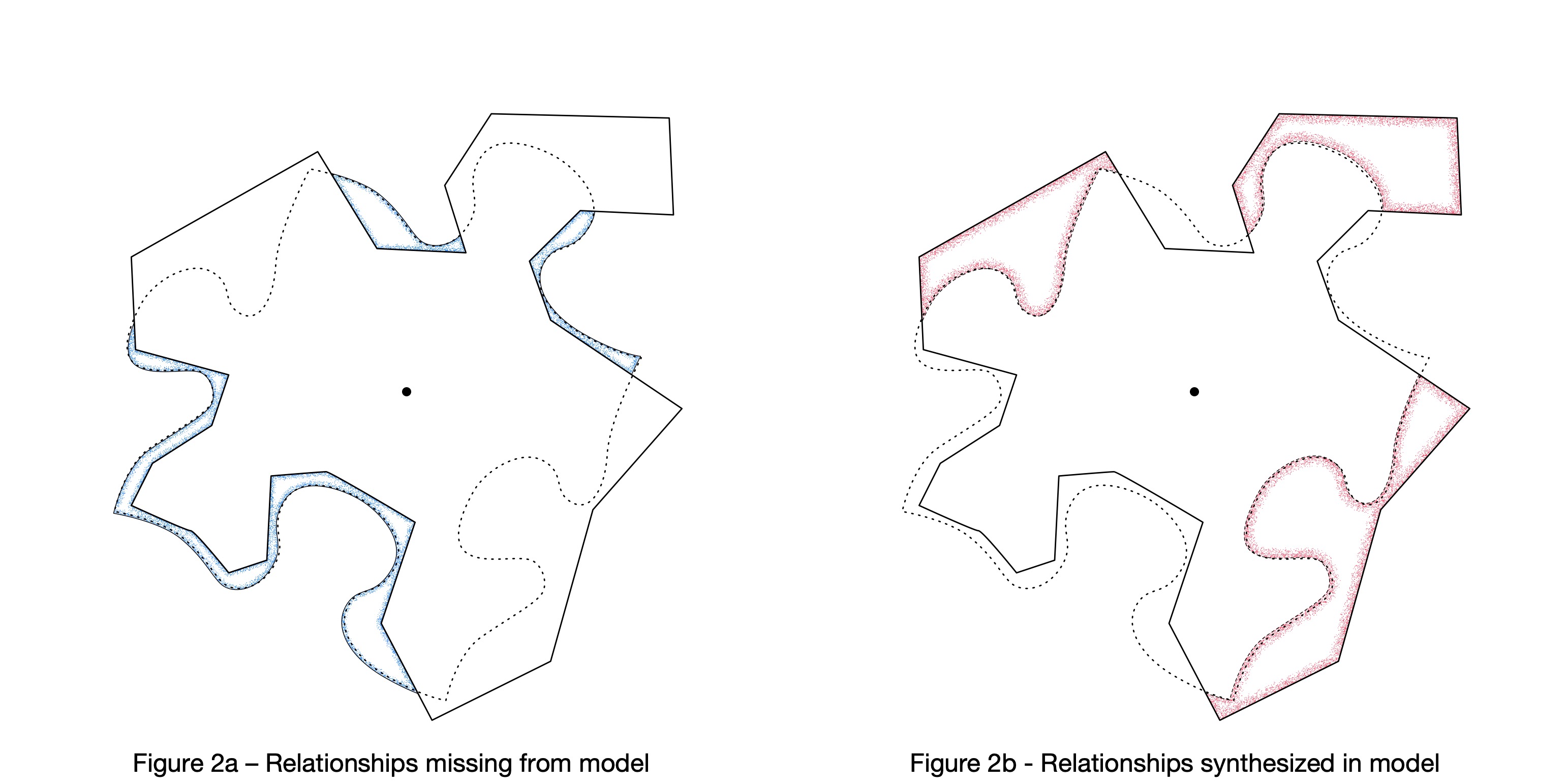
Like all models the LLM is inaccurate. It omits some relationships that are present in the training data, and it includes relationships that are not present. These deviations have important consequences for the quality of the outputs, as illustrated in the next set of figures.

Figure 2a illustrates regions where the training data includes actual text relationships that are not represented in the model as statistically likely. The model is less likely to generate such text, which can cause errors of omission.

Figure 2b illustrates regions containing statistically likely text relationships that do not appear in the training data. When the model generates text based on these relationships, the output is considered either insightful or hallucinatory depending on whether the text aligns with reality.

The output generation process

Once models are created, they are repeatedly executed to generate output from input without further modification. The output is generated one word at a time by calculating a set of likely candidates for the next word given the existing output and the original input prompt. A selected word from the candidates is added to the output, and this repeats until a stop condition is reached.

The key in the generation process is how the next word is selected from the candidates. For example, it might be selecting the next word for the phrase “Micky the dog took a ______” with candidate words “nap” probability 70%, “bone” probability 20%, and “selfie” probability 1%.

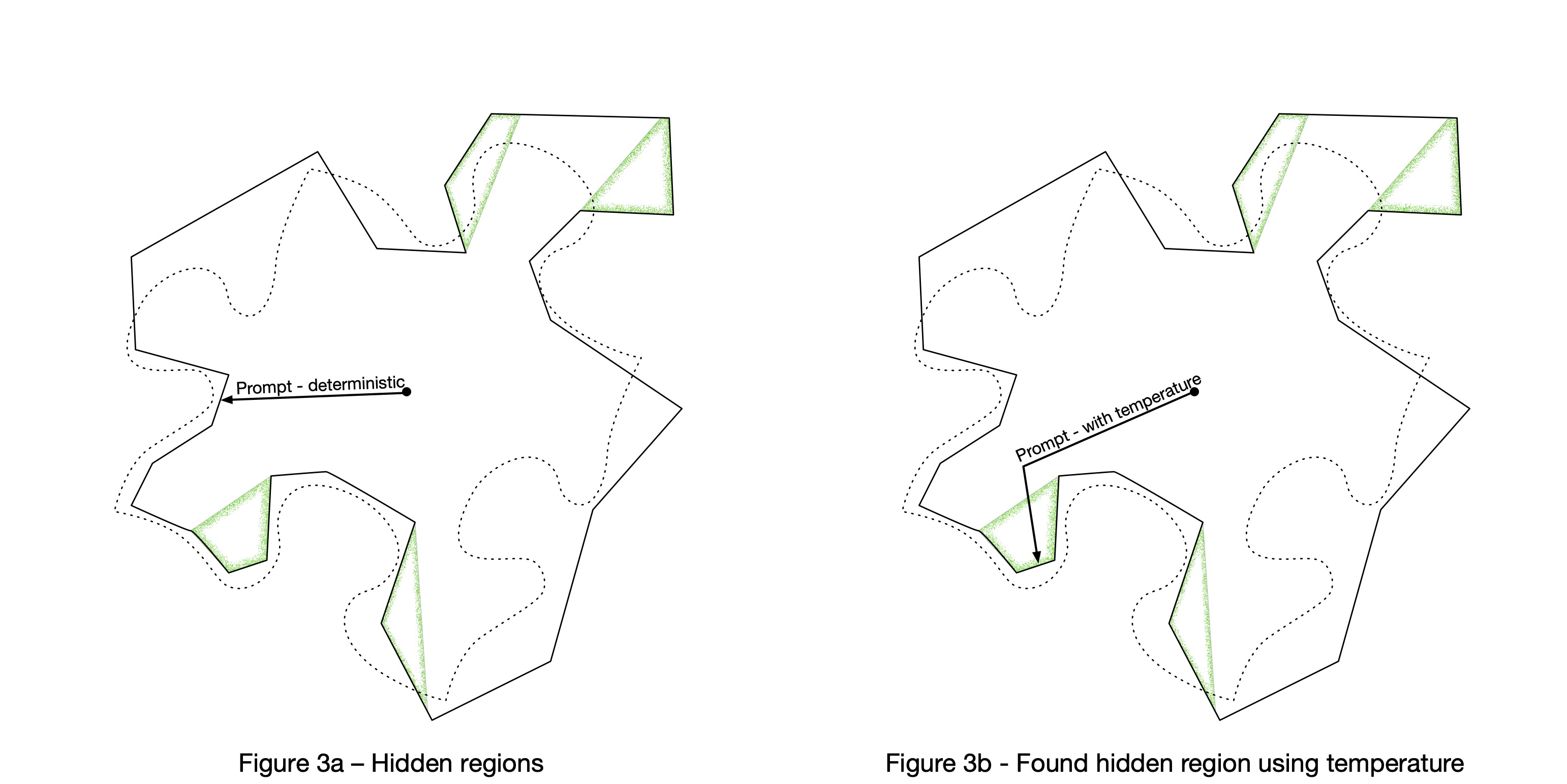
One approach is to always select the most likely word, but then the less likely words are never selected despite appearing in the training data. The model would have information that is never utilized, which increases the probability of error by omission. This is illustrated in Figure 3a showing a conceptual representation of deterministic word selection based on a prompt. The green regions of the model are relationships that cannot be utilized because the next-word selections have a low probability. Here we use a straight line to indicate using only the highest probability choice.

The actual approach used by LLMs today is to add a controlled amount of randomness to next-word selection so that all parts of the model can be utilized. In the example above, because the model gives “bone” a 20% probability one can expect it to be selected occasionally. Not as often as “nap”, but much more often than “selfie”. The amount of randomness is controlled by the temperature parameter, where higher values cause more variation. This is illustrated in Figure 3b, which shows how a non-zero temperature can explore additional regions of the model. The line’s turn represents using randomness to find lower-probability relationships.

Hallucinations

One of the consequences of using random numbers to override the model’s probabilities is that even very unlikely choices will occasionally show up in the output. Returning to our previous example, with a non-zero temperature you will sometimes get “Micky the dog took a selfie.” This could arise from the training data because dogs can take things and a “selfie” is in the class that can be taken, even though the LLM was never trained that a dog might do so. And now you have a classic LLM hallucination.

Or do you?

Perhaps Micky triggered a security camera in the room and his photo showed up on his owner’s phone. Perhaps there was a remote shutter release on the floor triggered by a paw. Of course these are not the most likely possibilities, but “selfie” is not offered as the most likely candidate to complete the generated sentence either. It’s difficult to say that the model is wrong in constructing this sentence. It might be a rare and valuable insight. Without additional input, insights and hallucinations are indistinguishable.

This raises the question of how to determine whether a model is hallucinating. Because there is a statistical likelihood associated with word choices as the output is constructed, it seems reasonable to compute the total probability of an output by multiplying the probabilities of the chosen words. The overall probability of various outputs can be compared, and if a particular output text has an unusually low probability then measures could be taken. For example, a chat user could be warned that the output might be fanciful.

It's a promising concept but unfortunately not a useful one. The statistical likelihoods associated with the word choices do not have a straightforward relationship with the actual probability of being “real”, or even explicit within the training data. These are better seen as local values that ensure outputs are consistent with the model. Researchers have experimented with many techniques to eliminate hallucinations without success, because at least some hallucinations are inherent.^[1]

The essential principle is this: One cannot determine whether a model is hallucinating by examining information only from within the model.

Volatility

Volatility is another challenge. Repeatedly providing a given input to an LLM returns different results each time. This property makes it difficult to build systems with LLM components because it is not possible to anticipate all possible responses, and therefore it is impossible to exhaustively test the results.

In theory it is possible to choose the seed for the LLM pseudo random number generator used for constructing outputs and create a predictable series of random numbers. With a fixed sequence of random numbers the LLM output will be entirely repeatable. Unfortunately in the real world the seed-based repeatability lasts only as long as the current version of the model. Even small model updates will change the results, sometimes greatly.

More importantly, a fixed sequence does not utilize the entire model despite once being randomly generated, just like the deterministic word selection described earlier. What if the fixed sequence happens to be one that generates unusably poor results? If the same word selections are always repeated then the model would never alter its bad output. Anything depending on these results would fail permanently. Oddly enough, it turns out that volatility is required to avoid being trapped!

The basic principle is this: It must be possible to execute the model again to obtain different output. The corollary is also important: There must be a means of evaluating LLM output quality outside of the model. If there is no way to evaluate the quality of the results then it would be impossible to know if execution should be repeated.

Instability

Instability is a further challenge. Having used a given LLM to process an input into an output, one finds that a different execution with a small change of input usually causes a significant change in the output. Instability is undesirable because it amplifies the effect of random input variations, such as noise, but it also complicates converging on a desired objective when the output is already close and only small changes are needed. Instability also leads to conflicting answers, which demonstrate model inaccuracy but also cause problems for external processes relying on LLM outputs.

For example, the following table shows the results of providing synonymous, non-identical prompts to a leading LLM today. Different prompts lead to calculating different numerical values during model execution, leading to dramatically different outputs. The table shows the closest match of summary paragraph between the executions, but the full outputs are even more different.

Note that the first output refers to breeds worldwide, while the second assumes domestic dogs. Adding “domestic” to the first prompt generated a new output reporting that an average domestic dog weighs “30 lb to 50 lb”, which still does not match the “30 lb to 70 lb” for domestic dogs in the original pair of responses. In this case increasing input specificity did not change output instability.

The essential principle is simply this: LLMs do not provide stable output.

Conclusions

Here are the essential LLM reliability principles articulated above:

1. One cannot determine whether a model is hallucinating by examining information only from within the model.
2. It must be possible to execute the model again to obtain different output.
3. There must be a means of evaluating LLM output quality outside of the model.
4. LLMs do not provide stable output.

Designing a reliable system that accommodates these characteristics is a significant challenge, but it can be done. I spent much of the last 12 months building an AI-based video editor for the AskHow micro course learning platform. Our third generation system works quite well, but we had to learn these principles from hard experience. I hope you find them useful.